[ML] 머신러닝 프로젝트 맛보기 1
실제 데이터로 작업하기
진행되는 실습에서는 StatLib 저장소에 있는 캘리포니아 주택 가격 데이터셋을 사용합니다. 이 데이터셋은 1990년 캘리포니아 인구조사 데이터를 기반으로 합니다.
큰 그림 보기
이 데이터에는 블록 그룹이라는 개념이 존재합니다. 블록 그룹은 미국 인구조사국에서 샘플 데이터를 발표하는 데 사용하는 최소한의 지리적 단위입니다. 하나의 블록 그룹은 보통 600~3,000명의 인구를 나타냅니다.
문제 정의
머신러닝은 문제를 어떻게 정의하는지로부터 시작됩니다. 문제를 정의하기 위해서는 비즈니스의 목적을 파악해야 합니다. 비즈니스의 목적에 따라 우리가 구현해야 할 머신러닝 시스템의 방향성이 결정됩니다.
머신러닝 시스템은 하나의 컴포넌트이며, 여러 컴포넌트가 서로 협력합니다.
현재 제가 담당하고 있는 컴포넌트가 있습니다. 이 컴포넌트의 출력은 하나의 신호로서 다른 컴포넌트의 입력으로 작용합니다. 즉, 제가 담당하고 있는 컴포넌트에서 예측이 올바르게 이루어져야 잇따라 나오는 컴포넌트에서 예측을 잘 수행할 수 있습니다. 한편, 머신러닝 시스템 사이에는 데이터를 저장하는 인터페이스가 존재합니다.
데이터 처리 컴포넌트들이 연속되어 있는 것을 데이터 파이프라인이라고 합니다.
머신러닝 시스템에는 데이터를 조작하고 변환할 일이 많아 이들을 하나의 컴포넌트로 추상화하고, 파이프라인을 구성합니다. 보통 컴포넌트들은 비동기적으로 동작합니다. 이는 각 컴포넌트가 완전히 독립적이라는 것을 의미하며, 하나의 컴포넌트가 다운되더라도 하위 컴포넌트는 문제가 발생한 컴포넌트의 마지막 출력을 사용해 계속 동작할 수 있다는 것을 뜻합니다.
현재 솔루션이 어떻게 구성되어 있는 지 파악해야 합니다.
구역 주택 가격을 전문가가 수동으로 추정한다는 것을 알게 됐습니다. 꽤나 복잡한 규칙에 의해 추정될 것입니다. 이는 시간과 비용이 많이 들 뿐더러, 추정 결과도 좋지 않습니다. 그래서 우리는 현재 솔루션으로부터 구역의 데이터를 기반으로 중간 주택 가격을 예측하는 모델을 훈련시키는 쪽이 유용하다고 판단할 수 있습니다.
이제 문제 정의를 해봅시다.
- 지도 학습(회귀)
- 레이블이 있는 훈련 데이터셋이 있으므로 이는 지도 학습에 속합니다.
- 주택 가격을 예측해야 하므로 회귀입니다.
- 예측에 사용되는 특성이 여러 개이므로 다중 회귀입니다.
- 각 구역마다 하나의 값을 예측하므로 단변량 회귀입니다.
- 배치 학습
- 이 시스템에 들어오는 데이터의 연속적인 흐름이 없으므로 배치 학습을 사용합니다.
성능 측정 지표
일반적으로 회귀 문제에 선호되는 성능 측정 지표는 RMSE(평균 제곱근 오차)입니다.
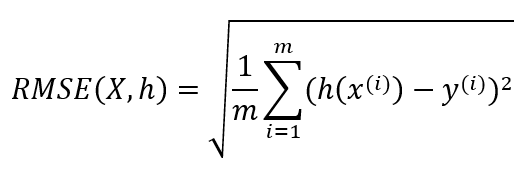
하지만 경우에 따라 다른 성능 측정 지표를 사용하기도 합니다. 예를 들어, 이상치로 보이는 구역이 많다면 MAE(평균 절대 오차)를 사용하는 것을 고려해볼 수 있습니다.
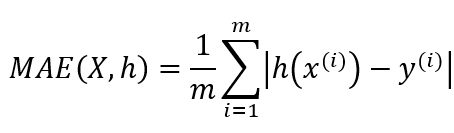
왜 상황에 따라 다른 성능 지표를 사용해야 할까요?
예측값의 벡터와 타깃값의 벡터 사이의 거리를 재는 방법을 Norm(노름)이라고 합니다.
Norm에는 다음과 같이 여러 가지가 있습니다.
- 유클라디안 노름(Euclidean norm 혹은 L2 norm)
- 우리가 흔히 아는 거리 개념입니다.
- RMSE가 이에 해당됩니다.
- 맨해튼 노름(Manhattan norm 혹은 L1 norm)
- 도시의 구획이 직각으로 나뉘어 있을 때 이 도시의 두 지점 사이의 거리를 측정하는 것과 같습니다.
- MAE가 이에 해당됩니다.
일반적으로 원소가 n개인 벡터 v의 Lk Norm을 다음과 같이 정의할 수 있습니다.
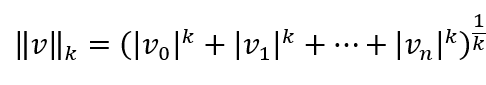
- L0 norm은 단순히 벡터에 있는 0이 아닌 원소의 수입니다.
- L_infinite norm은 벡터에서 가장 큰 절댓값이 됩니다.
노름의 지수 즉, k가 클수록 큰 값의 원소에 치우치며 작은 값은 무시됩니다. 데이터에 이상치가 많을 때에는 RMSE 보다 MAE를 사용하는 것이 그 이유입니다. 하지만 이상치가 매우 드물면 RMSE가 잘 맞아 일반적으로 사용됩니다.
가정 검사
마지막으로 여러 가정을 만들고 나열해서 검사를 진행합니다. 우리의 시스템에서 내놓는 출력이 다음 시스템의 입력으로 들어가는 상황을 떠올려봅시다. 우리는 회귀 알고리즘을 사용하여 가격을 예측했는데 다음 시스템에서는 카테고리를 입력으로 사용한다는 것입니다. 우리가 예측한 가격을 고가, 중가, 저가로 나누어서 사용하는 것이죠. 이렇게 되면 우리가 가격을 예측하는 건 별 의미가 없게 됩니다. 가정 검사는 이런 상황을 가정하고 검사를 진행하며 골치 아픈 문제들을 하나둘씩 제거해나가는 과정입니다.
데이터 가져오기
저는 아나콘다로 실습 환경을 설정하겠습니다. 아나콘다는 이미 설치했다는 가정 하에 진행하겠습니다. 우선 가상환경을 하나 만듭니다.
conda create -n already-on-my-hands python=3.7
already-on-my-hands 라는 이름으로 가상환경을 하나 만들었습니다. 가상환경을 활성화시킵니다.
conda activate already-on-my-hands
가상환경이 활성화되었습니다. 필요한 패키지들을 설치해줍니다.
conda install jupyter matplotlib numpy pandas scipy scikit-learn
잘 설치 되었는지 conda list 명령어로 확인해봅니다.
conda list jupyter
conda list matplotlib
conda list numpy
conda list pandas
conda list scipy
conda list scikit-learn
잘 설치되었습니다. 이제 주피터 노트북을 켜봅시다. 주피터 노트북의 기본 폴더는 users 폴더입니다. 별도의 폴더를 지정하고 싶으시면 cd 명령어로 위치시킨 후에 주피터 노트북을 켜시면 됩니다. 만약 중간에 한글 이름 때문에 명령어가 먹히지 않는다면 single quotation을 붙이면 됩니다.
cd C:\lws_workspace\'핸즈온 머신러닝 2판'\practices
jupyter notebook
주피터 노트북의 사용법에 대한 설명은 생략하겠습니다. 셀에 “Hello, world!”를 출력해봅시다.

잘 출력되는군요. 이제 데이터를 가져옵니다. csv 파일을 직접 가져올 수도 있지만 코드 레벨에서 csv 파일을 가져올 수도 있습니다. 정확히 말하면, tgz 파일을 내려받아 압축을 풀어 csv 파일을 얻는 겁니다. 편리성을 위해 함수를 다음과 같이 작성해서 사용합니다.
import os
import tarfile
import urllib
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml2/master/"
HOUSING_PATH = os.path.join("datasets", "housing")
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz"
def fetch_housing_data(housing_url=HOUSING_URL, housing_path=HOUSING_PATH):
os.makedirs(housing_path, exist_ok=True)
tgz_path = os.path.join(housing_path, "housing.tgz")
urllib.request.urlretrieve(housing_url, tgz_path)
housing_tgz = tarfile.open(tgz_path)
housing_tgz.extractall(path=housing_path)
housing_tgz.close()
fetch_housing_data()
이제 판다스로 데이터를 읽습니다.
import pandas as pd
def load_housing_data(housing_path=HOUSING_PATH):
csv_path = os.path.join(housing_path, "housing.csv")
return pd.read_csv(csv_path)
head()로 간단하게 확인해봅니다.
housing = load_housing_data()
housing.head()

info()로 데이터에 대한 간략한 설명과 전체 행 수, 각 특성의 데이터 타입과 널이 아닌 값의 개수 등을 확인합니다.
housing.info()
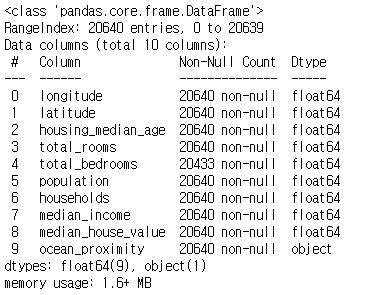
이제 몇 가지 분석을 해봅시다. 데이터는 총 20,640개이네요. 그리고 특성 중에 total_bedrooms만 누락된 데이터가 몇 개 있군요. 이는 나중에 별도의 처리를 할 필요가 있어 보입니다. 또한 ocean_proximity만 자료형이 object인 것을 확인합니다. value_counts()를 사용하여 ocean_proximity에 어떤 값들이 있고, 각 값마다 얼마나 있는지 확인해봅니다.
housing["ocean_proximity"].value_counts()

ocean_proximity는 위와 같은 값들을 가지고 있군요. ‘<1H OCEAN‘을 제일 많이 가지네요. 이제 describe()로 숫자형 특성의 요약 정보를 확인합니다.
housing.describe()
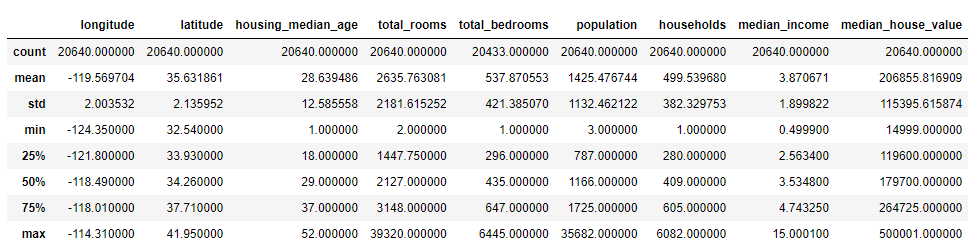
std는 값이 퍼져 있는 정도를 측정하는 표준편차를 나타냅니다. 25%(25번째 백분위수 혹은 제1사분위수), 50%(중간값), 75%(75번째 백분위수 혹은 제3사분위수) 행은 백분위수를 나타냅니다. 예를 들어, 25%의 구역은 housing_median_age가 18보다 작습니다.
hist()로 데이터의 형태를 빠르게 확인해봅시다. 이는 특성마다 그릴 수도 있고, 모든 숫자형 특성에 대해서도 그릴 수도 있습니다.
%matplotlib inline #주피터 노트북의 매직 명령
import matplotlib.pyplot as plt
housing.hist(bins=50, figsize=(20,15))
plt.show()
hist()는 matplotlib을 사용합니다. 결국 화면에 그래프를 그리기 위해 사용자 컴퓨터의 그래픽 백엔드를 필요로 합니다. 따라서 그래프를 그리기 전 matplotlib이 사용할 백엔드를 지정해줘야 하는데, 주피터만의 매직 명령 %matplotlib inline을 사용하면 편합니다. 참고로 주피터 노트북에서 그래프를 그릴 때 show()를 호출하는 것은 선택사항입니다.
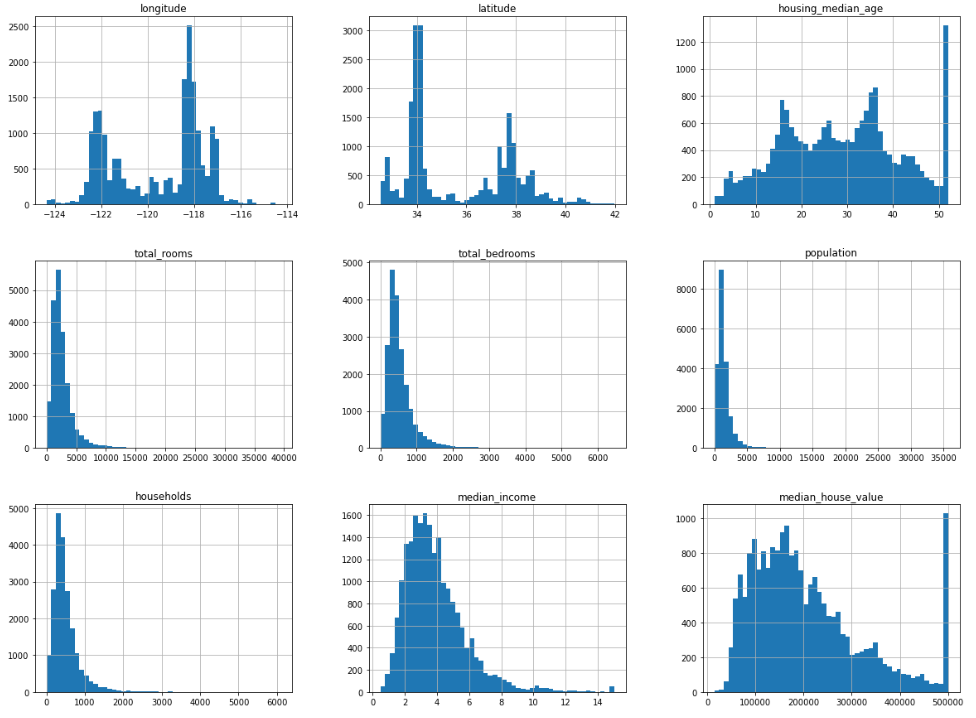
눈으로만 확인하고 넘어간다면 오산입니다. 같이 분석해봅시다.
- median_income 특성은 US 달러로 표현되어 있지 않습니다.
- 상한이 15, 하한이 0.5가 되도록 만들어져 있습니다. 즉, 전처리가 되어 있는 데이터입니다.
- 머신러닝에서는 이런 데이터를 다루는 것이 흔하지만, 왜 이렇게 계산이 된 건지는 반드시 이해하고 있어야 합니다.
- housing_median_age와 median_house_value 역시 상한과 하한이 존재합니다.
- median_house_value는 타깃으로 사용되기 때문에 심각한 문제가 발생할 수 있습니다. 머신러닝 알고리즘이 한곗값을 넘어가지 않도록 학습될 수 있기 때문입니다.
- 한곗값을 넘어가더라도 정확한 예측값이 필요하면 어떻게 해야 할까요?
- 한곗값 밖의 구역에 대한 정확한 레이블을 구합니다.
- 훈련 데이터셋에서 한계값을 넘는 구역을 제거합니다. 한곗값을 넘는 값에 대한 예측은 어차피 평가가 좋지 않을 것이므로, 테스트 데이터셋에서도 제거합니다.
- 특성들의 스케일이 서로 다릅니다.
- 이는 특성 스케일링을 사용하면 됩니다. 이후에 나오는 내용에서 확인합니다.
- 대부분의 히스토그램의 꼬리가 가운데에서 오른쪽으로 더 멀리 뻗어 있습니다.
- 이를 꼬리가 두껍다고 표현합니다.
- 이런 형태는 머신러닝 알고리즘에서 패턴을 찾기 어렵게 만듭니다.
- 이 문제는 특성들을 종 모양의 분포가 되도록 변형시킴으로써 해결할 수 있습니다. 이것도 이후에 나오는 내용에서 확인합니다.
테스트 데이터셋 만들기
우리가 관심을 가지고 분석해야 할 대상은 훈련 데이터셋일 뿐입니다. 테스트 데이터셋에는 관심을 끄는 게 머신러닝 시스템이 일반성을 띠는 데 도움이 됩니다. 이와 관련해서 데이터 스누핑 편향이라는 용어가 등장합니다. 이는 테스트 데이터셋이 유출되어 그 내재된 패턴에 속아 우리의 머신러닝 모델이 특정되는 현상을 의미합니다. 다시 한 번 강조하지만, 머신러닝은 일반화입니다. 일반화를 잘 하기 위해서는 성능 평가에 사용되는 데이터가 일반성을 지니어야 합니다. 아무리 일반성이 뛰어난 데이터라고 해도 우리가 그 데이터를 들여다 보게 된 시점 이후로는 더 이상 그 데이터는 일반성을 지니지 않게 됩니다.
이제 주어진 데이터셋으로부터 테스트 데이터셋을 분리해봅시다.
import numpy as np
def split_train_test(data, test_ratio):
shuffled_indices = np.random.permutation(len(data))
test_set_size = int(len(data) * test_ratio)
test_indices = shuffled_indices[:test_set_size]
train_indices = shuffled_indices[test_set_size:]
return data.iloc[train_indices], data.iloc[test_indices]
train_set, test_set = split_train_test(housing, 0.2)
print("train_set: {}".format(len(train_set)))
print("test_set: {}".format(len(test_set)))

비율만큼 잘 분리되네요. 하지만, 위 코드를 다시 실행시키면 비율만 같을 뿐, 다른 테스트 데이터셋이 생성됩니다. 그래서 동일 테스트 데이터셋을 생성하기 위해서 일반적으로는 다음과 같이 두 가지 방법을 사용합니다.
- 테스트 데이터셋을 저장하고, 다음 실행에서 이를 불러오는 방법
- 항상 같은 난수 인덱스가 생성되도록 초깃값을 지정하는 방법
np.random.seed(42)
하지만, 데이터셋에 데이터가 추가된다면 위 방법들은 여전히 괜찮을까요? 우리는 앞서, 테스트 데이터셋은 들여다 보지 않기로 했습니다. 하지만, 데이터가 추가 된다면 이전 훈련에 사용했던 데이터가 테스트 데이터셋에 포함될 수 있습니다. 그래서, 우리는 데이터 자체에 식별자(정확히 말하면, 식별자의 해시값)를 사용하여 동일 데이터를 유지할 수 있습니다. 즉, 데이터가 추가되어도 이전 훈련에 사용된 데이터는 테스트 데이터셋에 포함되지 않습니다.
from zlib import crc32
def test_set_check(identifier, test_ratio):
return crc32(np.int64(identifier)) & 0xffffffff < test_ratio * 2**32
def split_train_test_by_id(data, test_ratio, id_column):
ids = data[id_column]
in_test_set = ids.apply(lambda id_: test_set_check(id_, test_ratio))
return data.loc[~in_test_set], data.loc[in_test_set]
식별자 컬럼이 없으므로, 인덱스를 사용합니다. housing.reset_index()로 index 컬럼이 만들어진 것을 확인합니다.
housing.reset_index()
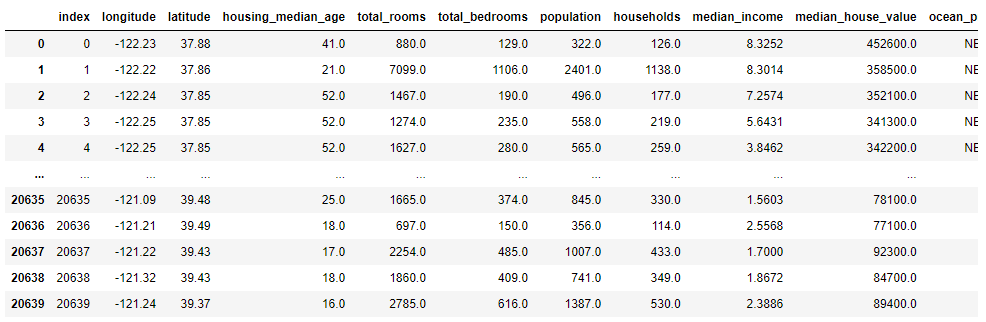
housing_with_id = housing.reset_index()
train_set, test_set = split_train_test_by_id(housing_with_id, 0.2, "index")
print("[train_set]\n{}".format(train_set['median_house_value'][:5]))
print("[test_set]\n{}".format(test_set['median_house_value'][:5]))

데이터를 추가하고 위 코드를 여러 번 실행해도, 이전 훈련에 사용된 데이터가 테스트 데이터셋에 포함되는 상황은 발생하지 않을 것입니다.
만약, 식별자로 index를 사용하는 것이 위험하다면, 주어진 특성으로 식별자를 생성해서 사용하는 방법도 있습니다.
사이킷런은 데이터셋을 여러 서브셋으로 나누는 다양한 방법을 제공합니다. 가장 간단한 함수는 train_test_split입니다.
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(housing, test_size=0.2, random_state=42)
print("[train_set]\n{}".format(train_set['median_house_value'][:5]))
print("[test_set]\n{}".format(test_set['median_house_value'][:5]))

우리는 지금까지 무작위 샘플링 방식을 보았습니다. 지난 글에서 좋은 데이터를 쓰기 위한 방법 중 하나로 대표성을 띠는 데이터를 사용해야 한다고 언급했었습니다. 이는 테스트 데이터셋에서도 동일하게 적용됩니다. 무작위 샘플링 방식은 테스트 데이터셋이 대표성을 띠는 데 아무런 도움을 주지 않습니다. 따라서 우리는 계층적 샘플링 방식을 사용하여 테스트 데이터셋이 대표성을 띠도록 해야 합니다. 계층적 샘플링 방식은 전체 모수를 동질의 계층(strata)으로 나누고, 계층별로 샘플링하는 것입니다.
동질의 계층이라도 마구잡이로 나누면 안 됩니다.
개별 계층에 충분한 샘플 수가 있어야 합니다. 어느 계층은 샘플 수가 많고, 어느 계층은 샘플 수가 적다면 적은 쪽의 중요도를 추정하는 데 있어서 편향이 발생할 것입니다. 계층 샘플링을 위해서는 사이킷런의 StratifiedShuffleSplit을 사용합니다.
먼저 income_cat 특성의 비율을 확인해보겠습니다.
housing["income_cat"] = pd.cut(housing["median_income"], bins=[0., 1.5, 3.0, 4.5, 6., np.inf], labels=[1, 2, 3, 4, 5])
housing["income_cat"].hist()
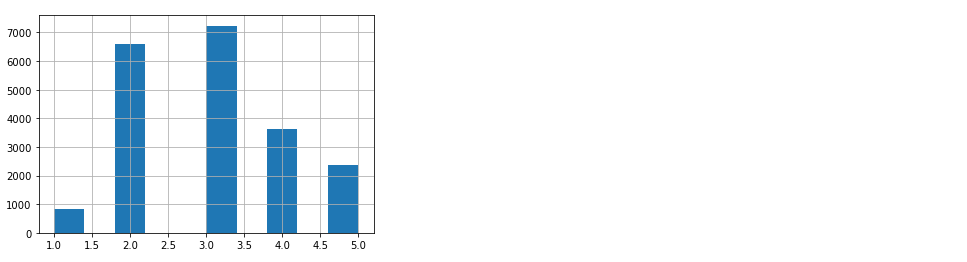
다음으로 사이킷런의 StratifiedShuffleSplit을 사용합니다.
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(housing, housing["income_cat"]):
strat_train_set = housing.loc[train_index]
strat_test_set = housing.loc[test_index]
strat_test_set["income_cat"].hist()
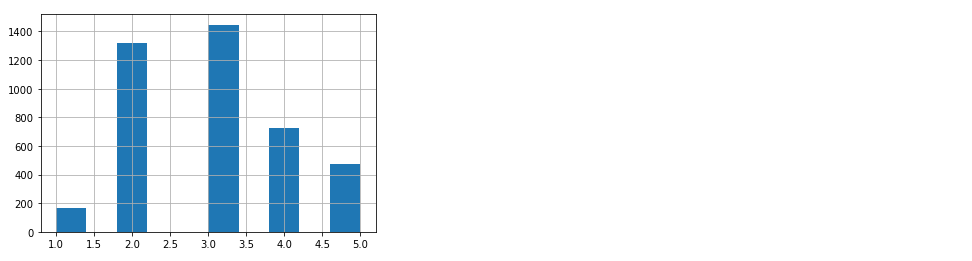
좋습니다. 데이터의 비율이 거의 같으므로, 계층 샘플링이 정상적으로 수행된 것을 알 수 있습니다.
데이터 이해를 위한 탐색과 시각화
실습 중 훈련 세트를 손상시키지 않기 위해 복사본을 만들어 사용하겠습니다.
housing = strat_train_set.copy()
지리적 데이터 시각화
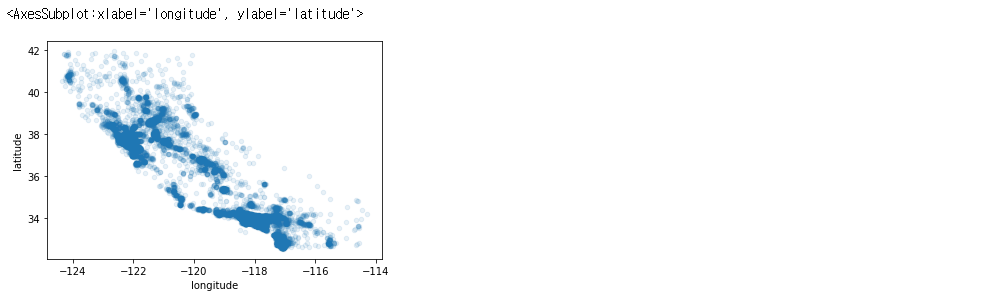
데이터를 시각화해봅시다. 위도와 경도 특성을 가지고 있으니 시각화하기에 좋습니다. alpha를 0.1로 주어 (어차피 봐봤자 무슨 지역인지 모르긴 하지만) 데이터가 어느 지역에 밀집되어 있는지까지 확인합니다.
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1)
주택 가격을 나타내보겠습니다. 원의 반지름은 구역의 인구(s)를 나타내고, 색상은 가격(c)을 나타냅니다.
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4, s=housing["population"]/100, label="population", figsize=(10,7), c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True, sharex=False)
plt.legend()
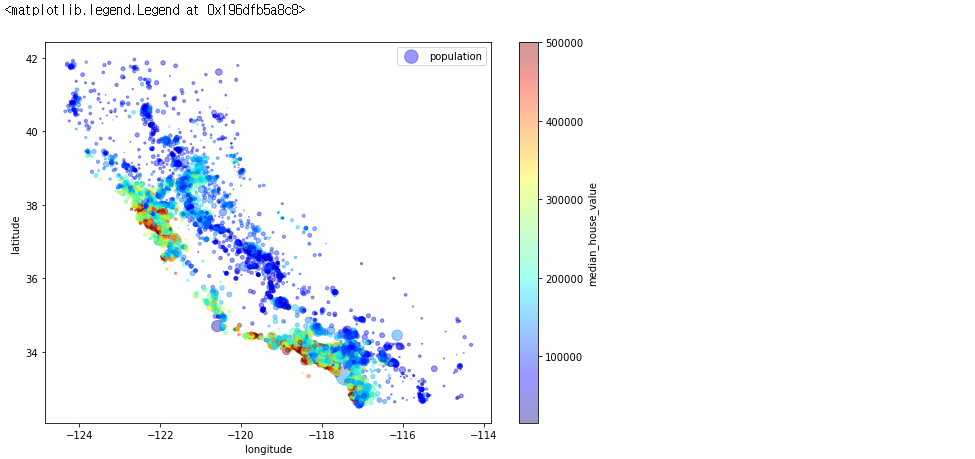
인구 밀도가 낮은 지역이 주택 가격이 높네요. 또한 책에서 주택 가격이 높은 지역들은 해안가 주변이라고 합니다. 이상, 시각화로 이러한 사실들을 알 수 있었습니다.
Q. 주요 군집은 어떻게 찾는 걸까요?
상관관계 조사
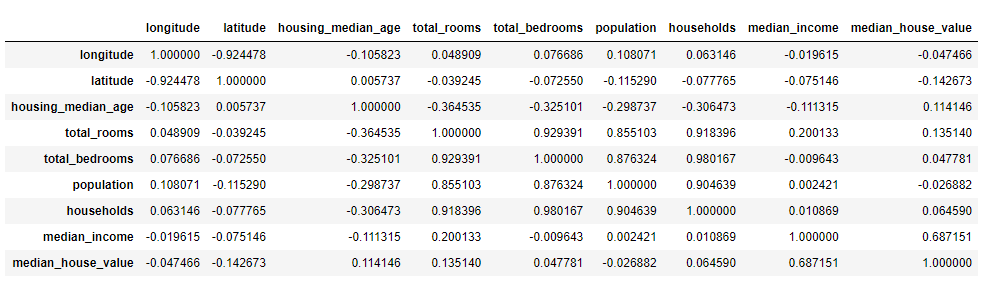
좋은 데이터를 사용하기 위해서는 관련이 높은 특성의 데이터를 사용해야 한다고 1장에서 다뤄본 적이 있습니다. corr()로 각 특성별로 다른 특성과의 상관관계 크기를 확인할 수 있습니다.
corr_matrix = housing.corr()
corr_matrix
sort_values()로 median_house_value와 다른 특성과의 상관관계 크기를 내림차순으로 확인해봅시다.
corr_matrix["median_house_value"].sort_values(ascending=False)

상관관계의 범위는 -1~1입니다. 상관관계 크기를 나타내는 값을 상관계수라고 합니다. 상관계수가 1에 가까우면 상관관계가 높다는 것이고, -1에 가까우면 상관관계가 낮은 걸 넘어 오히려 반대되는 관계임을 뜻합니다. 그리고 0에 가까우면 선형적인 상관관계가 없다는 뜻입니다. 이를 통해, 상관계수는 선형적인 상관관계만을 측정한다는 것을 알 수 있습니다.
scatter_matrix()로 특성 사이의 상관관계를 확인할 수도 있습니다. 사용해보겠습니다.
from pandas.plotting import scatter_matrix
attributes = ["median_house_value", "median_income", "total_rooms", "housing_median_age"]
scatter_matrix(housing[attributes], figsize=(12, 8))
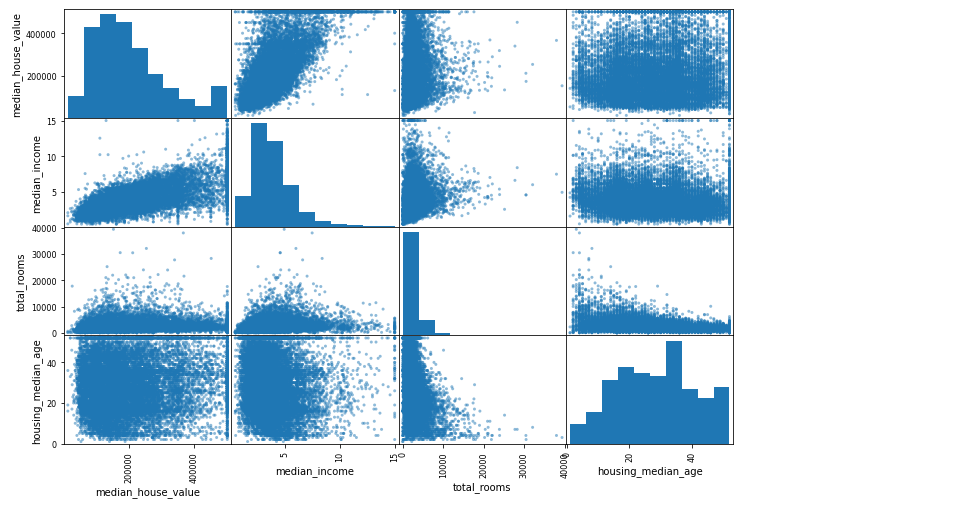
median_house_value를 예측하는 데 가장 유용할 거 같은 특성은 median_income입니다. 그 이유는 다음과 같습니다.
- 상관관계가 매우 강합니다.
- 위쪽으로 향하는 경향을 갖습니다.
- 포인트들이 비교적 밀집되어 있습니다.
- 가격 제한값이 500,000 달러에서 수평선으로 잘 보입니다.
- 제한값이 아닌 350,000 달러와 280,000에도 희미하게 수평선이 보이므로 나중에 이런 데이터는 전처리가 필요합니다.
특성 조합
특정 구역의 방 개수는 얼마나 많은 가구 수가 있는지 모른다면 그 자체로는 그다지 유용하지 않습니다. 즉, 개별적으로는 그다지 의미 없던 특성들을 조합하면 의미 있는 특성이 됩니다. 이 작업을 진행해보죠.
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"] = housing["population"]/housing["households"]
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)

조합한 특성의 상관계수가 개별 특성의 상관계수보다 더 높습니다.
지금까지 데이터 이해를 위한 탐색을 진행했습니다. 이 탐색 단계는 완벽하지 않으며, 데이터로부터 빠르게 통찰을 얻는 것이 목적입니다. 이 프로토타입을 실행하여, 다시 탐색 단계로 돌아오면 더 많은 통찰을 얻을 수 있습니다. 머신러닝 프로젝트에서는 빠른 프로토타이핑과 반복적인 프로세스가 권장됩니다.
Uploaded by Notion2Tistory v1.1.0